Overview

The Sequencer is an algorithm designed to automatically reveal the main trend or sequence in a dataset, if it exists. To do so, it reorders a collection of objects to produce the most elongated manifold describing their similarities estimated in a multi-scale and multi-metric manner. This process can generically reveal the main trend in arbitrary datasets.
For a quick overview, see simple examples and scientific discoveries made with the algorithm.

Concept

Most of the time, objects in a dataset are not ordered in any interesting manner. If these objects follow a trend, it should be possible to order the set meaningfully and, as a result, reveal the underlying trend. To automatically search for this trend, the algorithm proceeds as follows:

Given a dataset with N objects, one can compute a distance matrix D characterizing the (dis)similarity between all pairs of objects. The distance matrix D describes a fully-connected graph, encoding all possible connections between its nodes, weighted by the corresponding distances.
An important subset of this graph is given by its Minimum Spanning Tree. It connects all the nodes and minimizes the total distance between them. Its shape carries fundamental information about the data. If the objects do not exhibit any correlation, the Minimum Spanning Tree will not display any preferred orientation. However, if it is found to be elongated, then an underlying trend does exist in the dataset. Traversing the sequence provided by the minimum spanning tree then provides us with a way to meaningfully order the set of objects and reveal the detected trend.

Generic search for trends

One challenge in finding a trend in a dataset is being able to “look” at the data from the right point of view. For example, computing a distance matrix for a dataset requires the use of a metric and the choice of a scale. In order to be as generic as possible, one should (i) consider an ensemble of metrics and scales, (ii) identify which carry relevant information about the existence of an underlying trend and (iii) combine them meaningfully. To do so, the algorithm proceeds as follows:

It evaluates distance matrices using a collection of metrics:

the Euclidean Distance
the (entropy based) Kullback-Leibler Divergence
the Monge-Wasserstein or Earth Mover Distance
the Energy Distance.

In addition, the algorithm breaks the objects into parts using a binary tree, all the way down to parts of minimum twenty pixels.
For each metric and each part, it computes distances between all pairs of objects. The algorithm estimates the level at which a continuous trend is present in the dataset by using the elongation of the corresponding distance matrix minimum spanning trees.
The algorithm then aggregates information from all relevant scales and metrics by constructing an elongation-weighted distance matrix. The minimum spanning tree of this combined distance matrix provides an ordering of the objects in the dataset that corresponds to the final sequence.

This approach is designed to define a view of the data, through the combination of different metrics and scales, that leads to the most elongated manifold.

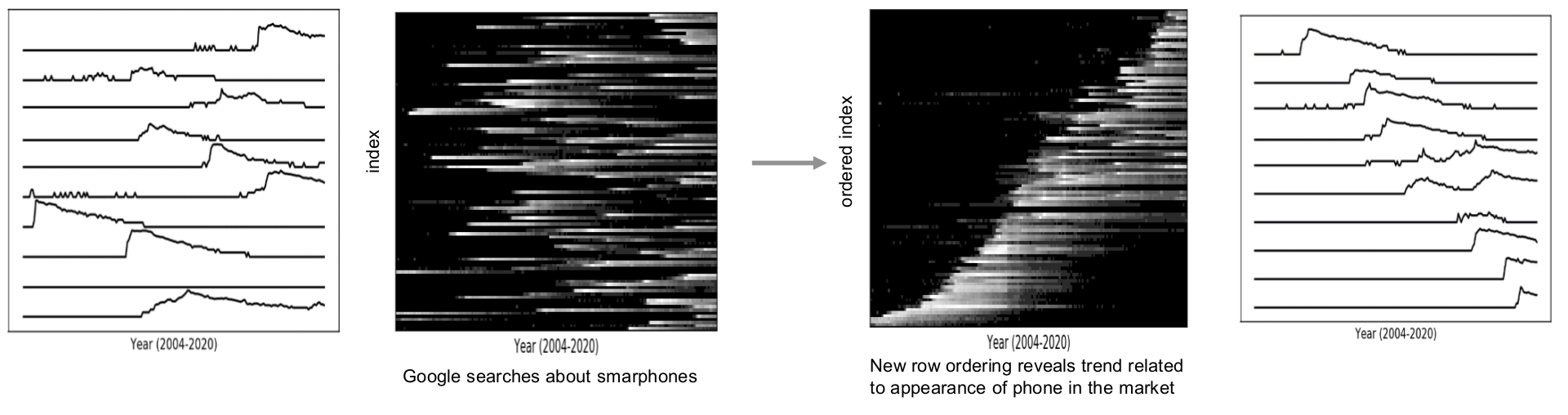
Example showing the automatic ordering of time series

showing the number of Google searches for different smartphones.

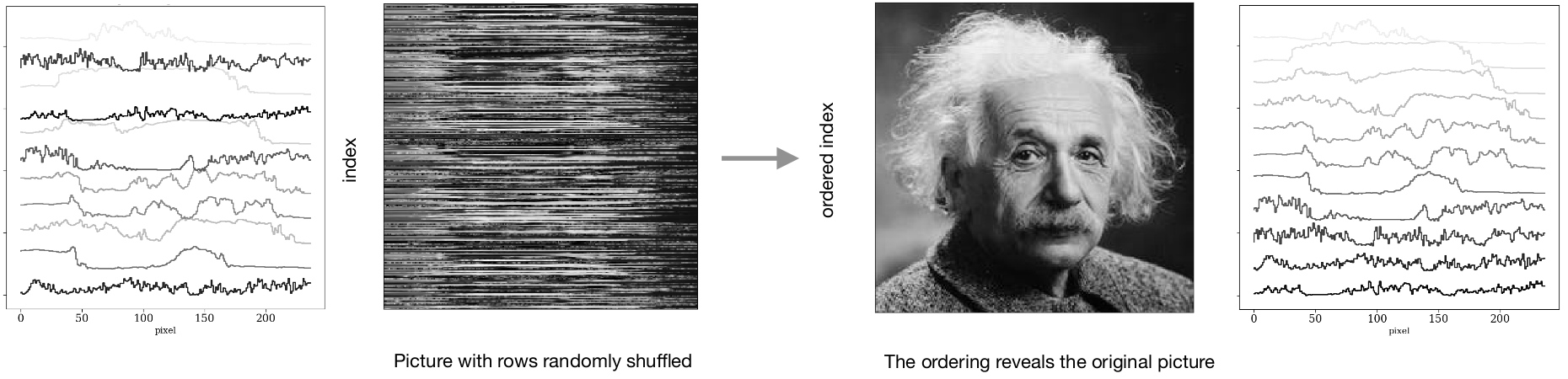
Example showing the automatic ordering of time series showing the reconstruction

of an image for which rows were randomly shuffled.

Paper and code

The paper introducing the algorithm: “Extracting the main trend in a dataset” (Baron & Ménard 2020) [link]
The source code is available on GitHub at: https://github.com/dalya/Sequencer
The pseudo-code is given here.

Credits

Concept & algorithm: Dalya Baron1 & Brice Ménard2

Online platform: Manuchehr Taghizadeh-Popp2

Affiliations: (1) Tel Aviv University, (2) Johns Hopkins University

Support: This project has been supported by the Packard Foundation and the generosity of Eric and Wendy Schmidt by recommendation of the Schmidt Futures program. This online platform uses resources provided by the SciServer project from the Institute for Data Intensive Engineering and Science.